Методы Монте-Карло

Примеры

Приближенное вычисление числа $\pi$

Пусть $(X, Y)$ -- случайный вектор, равномерно распределенный на квадрате $\Omega = (-1, 1) \times (-1, 1)$. Плотность распределения: $p(x, y) = \dfrac{1}{4}$ в $\Omega$.

Пусть $C$ -- единичный круг с центром в точке $(0, 0)$. Вероятность того, что случайный вектор попадёт в круг, равна $$P\{(X,Y) \in C\} = \iint\limits_C p(x,y) dxdy = \frac{\pi}{4}.$$

Определим также случайную величину $Z$, равную 1, если $(X,Y) \in C$, и 0 в противном случае. Очевидно, что $E[Z] = \dfrac{\pi}{4}$.

Пусть $Z_1, Z_2, \ldots, Z_N$ -- повторная выборка, т.е. совокупность попарно независимых и одинаково распределенных (с таким же распределением, как $Z$) случайных величин. Согласно закону больших чисел, $$\frac{Z_1 + Z_2 + \ldots + Z_N}{N} \stackrel{P}{\longrightarrow} \frac{\pi}{4},$$ то есть $$\forall \varepsilon > 0 \;:\; P\left(\left|\frac{Z_1 + Z_2 + \ldots + Z_N}{N} - \frac{\pi}{4}\right| \geq \varepsilon\right) \to 0, \; N \to \infty.$$

Для приближенной оценки числа $\pi$ сгенерируем $N$ пар случайных величин $a_k, b_k$ с распределением $R(0,1)$, затем найдем $x_k = 2a_k - 1$, $y_k = 2b_k - 1$ и положим $z_k = 1$, если $x_k^2 + y_k^2 < 1$, и $z_k = 0$ в противном случае.

Оценка числа $\pi$: $$\widehat\pi_N = \frac{4}{N}\sum_{k=1}^N z_k.$$

Используем пакет GNU Octave. Датчик случайных чисел -- функция rand, в которой реализован алгоритм "Вихрь Мерсенна" с периодом $2^{19937}-1$.

# Оценка числа pi
# N -- количество точек
function ret = pi_est(N)
  s = 0;
  for i = 1 : N
    p = 2 * rand(1, 2) - 1;
    s += p(1) ^ 2 + p(2) ^ 2 < 1;            
  endfor
  ret = 4 * s / N;
endfunction

Далее возьмем значения $N = 1000, 2000, 3000, \ldots, 25000$ и для каждого $N$ проведем 5 вычислений оценки числа $\pi$. Результаты представлены на следующем графике.

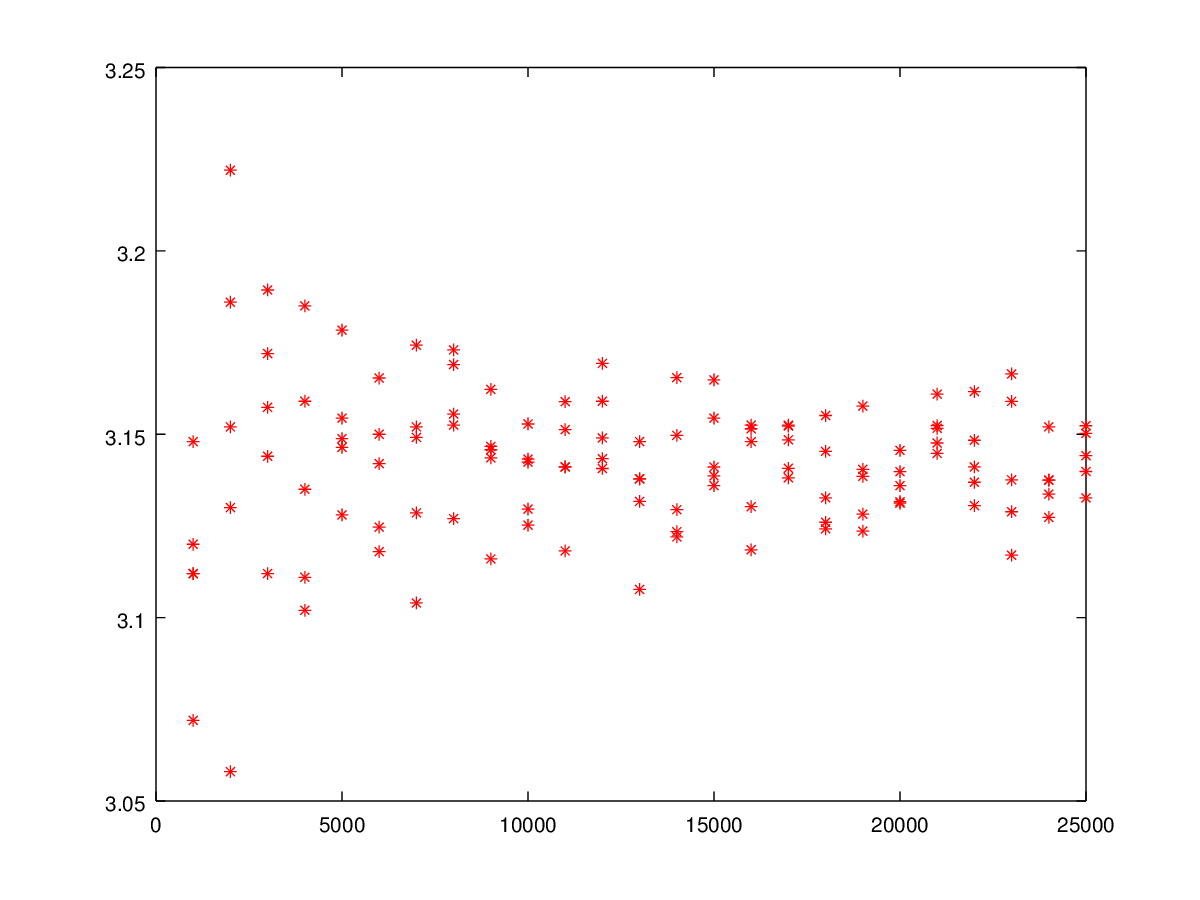
Также для каждого $N$ посчитаем по 5 оценкам среднеквадратичное отклонение от числа $\pi$.

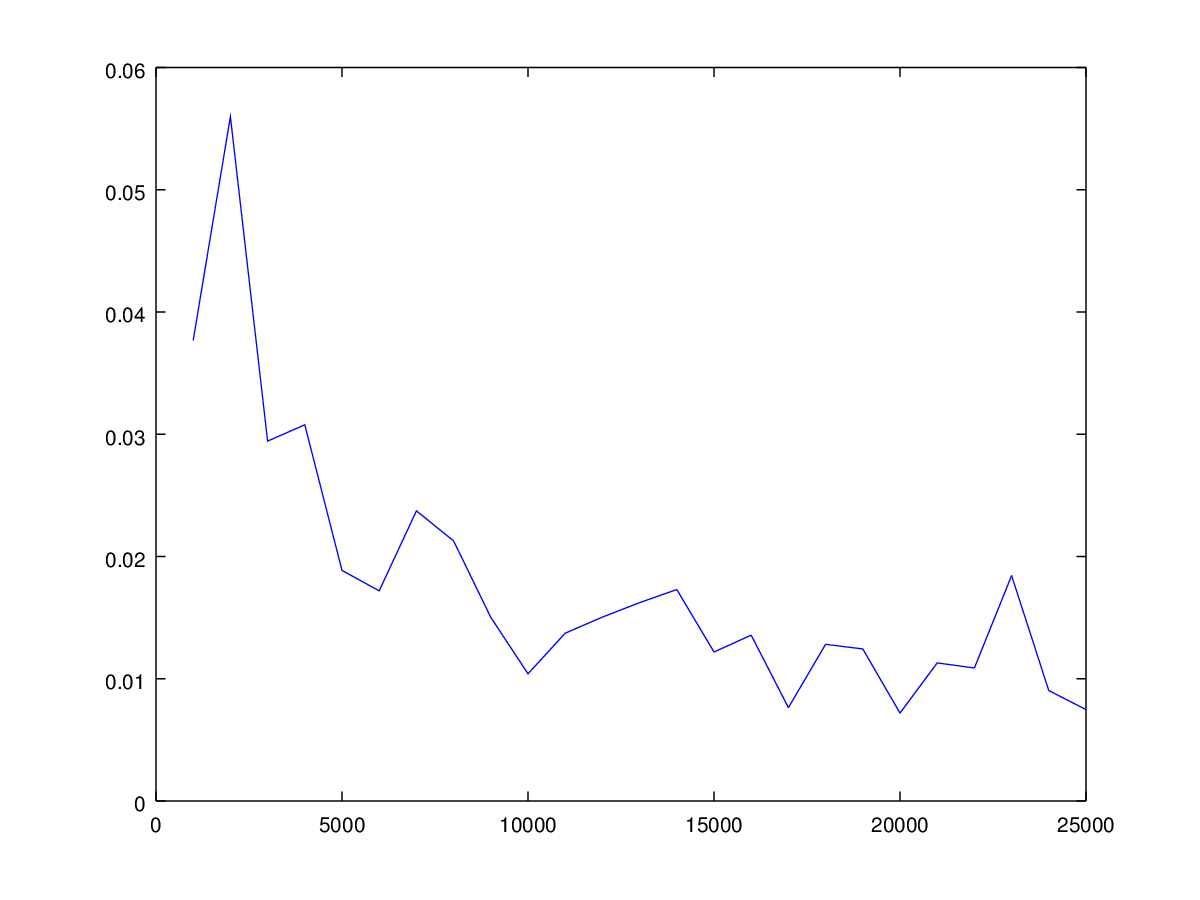
Отметим, что при каждом запуске программы будут получаться разные графики ввиду случайности.

Код:

clear all
more off

Nval = 1000 : 1000 : 25000;
M = 5;
for i = 1 : length(Nval)
  N = Nval(i)
  rms = 0;
  for k = 1 : M
    est = pi_est(N);
    rms += (est - pi) ^ 2;
    px(i, k) = N;
    py(i, k) = est;
  endfor
  rms_vec(i) = sqrt(rms / M);
endfor

figure
plot(Nval, rms_vec);

px_ = vec(px')';
py_ = vec(py')';
figure
plot(px_, py_, "r*");

Приближенное вычисление определенного интеграла

Источники:

1. Бахвалов, Жидков, Кобельков "Численные методы"
2. Modest Radiative heat transfer, 2013.

Требуется найти определенный интеграл $\int_a^b f(x)\,dx$.

Пусть $X$ -- случайная величина с равномерным распределением на $(a, b)$. Плотность распределения: $$p_X(x) = \frac{1}{b-a}, \;\; x \in (a, b).$$

Введем случайную величину $Y = f(X)$, тогда $$E[Y] = \int_a^b f(x) p_X(x)\,dx = \frac{1}{b-a}\int_a^b f(x)\,dx.$$

Таким образом, $$\int_a^b f(x)\,dx = (b-a)E[Y].$$

Для приближенного вычисления интеграла рассмотрим $N$ попарно независимых, одинаково распределенных (с распределением, как у $Y$) случайных величин $Y_1, Y_2, \ldots Y_N$. Положим $Y_k = f(X_k)$, здесь $X_k \sim R(a,b)$ -- попарно независимые сл.в.

В силу закона больших чисел $$\frac{Y_1 + Y_2 + \ldots + Y_N}{N} \stackrel{P}{\longrightarrow} E[Y].$$

Алгоритм:

1. Сгенерировать выборку с распределением $R(a, b)$ по формуле $x_k = a + (b-a)r_k$, где $r_k$ -- выборка с распределением $R(0,1)$.
2. Найти $\dfrac{b-a}{N}\displaystyle\sum_{k=1}^N f(x_k)$.

Код:

# Вычисление интеграла от f на (a, b) при помощи выборки длины N
function ret = calc_integral(f, a, b, N)
  s = 0;
  for i = 1 : N
    x = a + rand * (b - a);
    s += f(x);
  endfor
  ret = (b - a) / N * s;
endfunction

Пример: $\int_0^{\pi/2} \sin x\, dx = 1$.

Проведем такие же вычисления, как и для числа $\pi$.

Значения интеграла в зависимости от $N$:

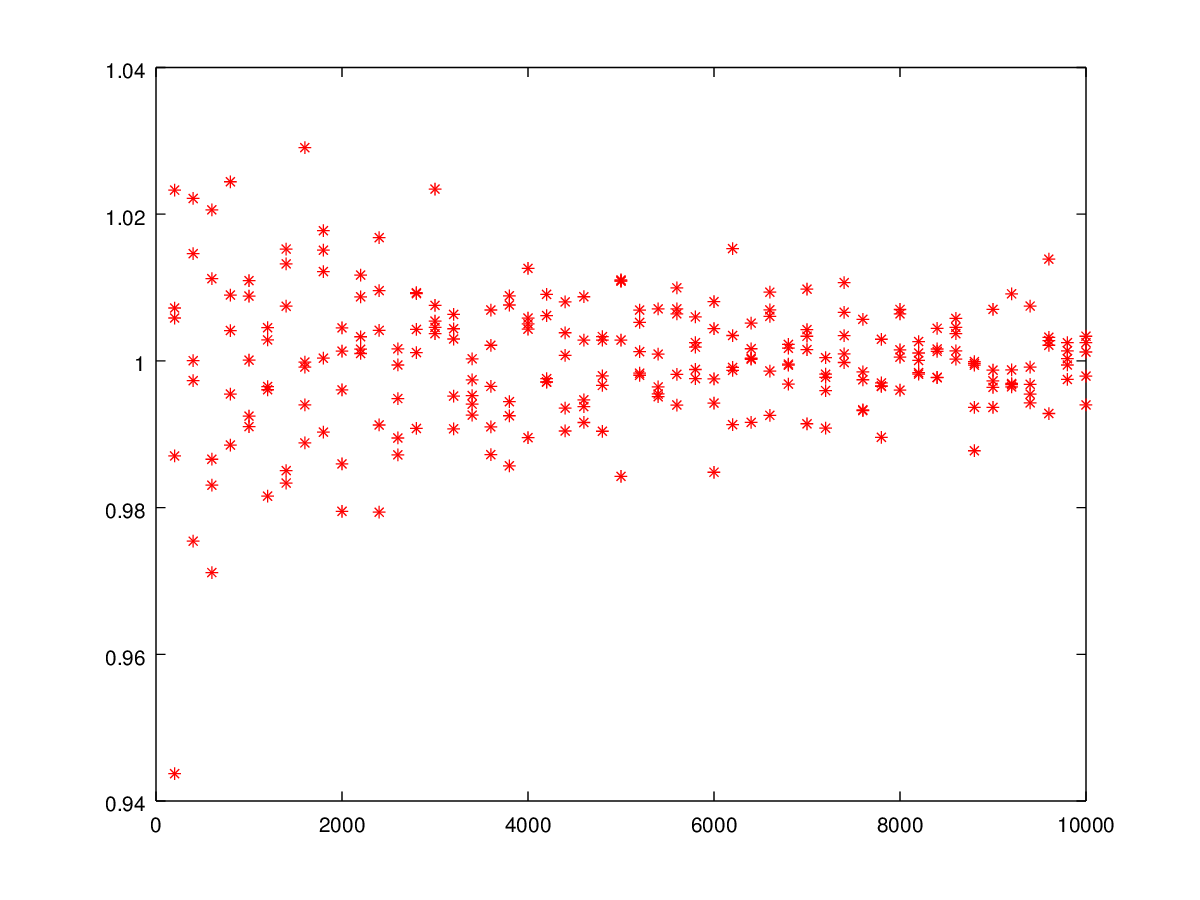
Среднеквадратичное отклонение от точного значения интеграла:

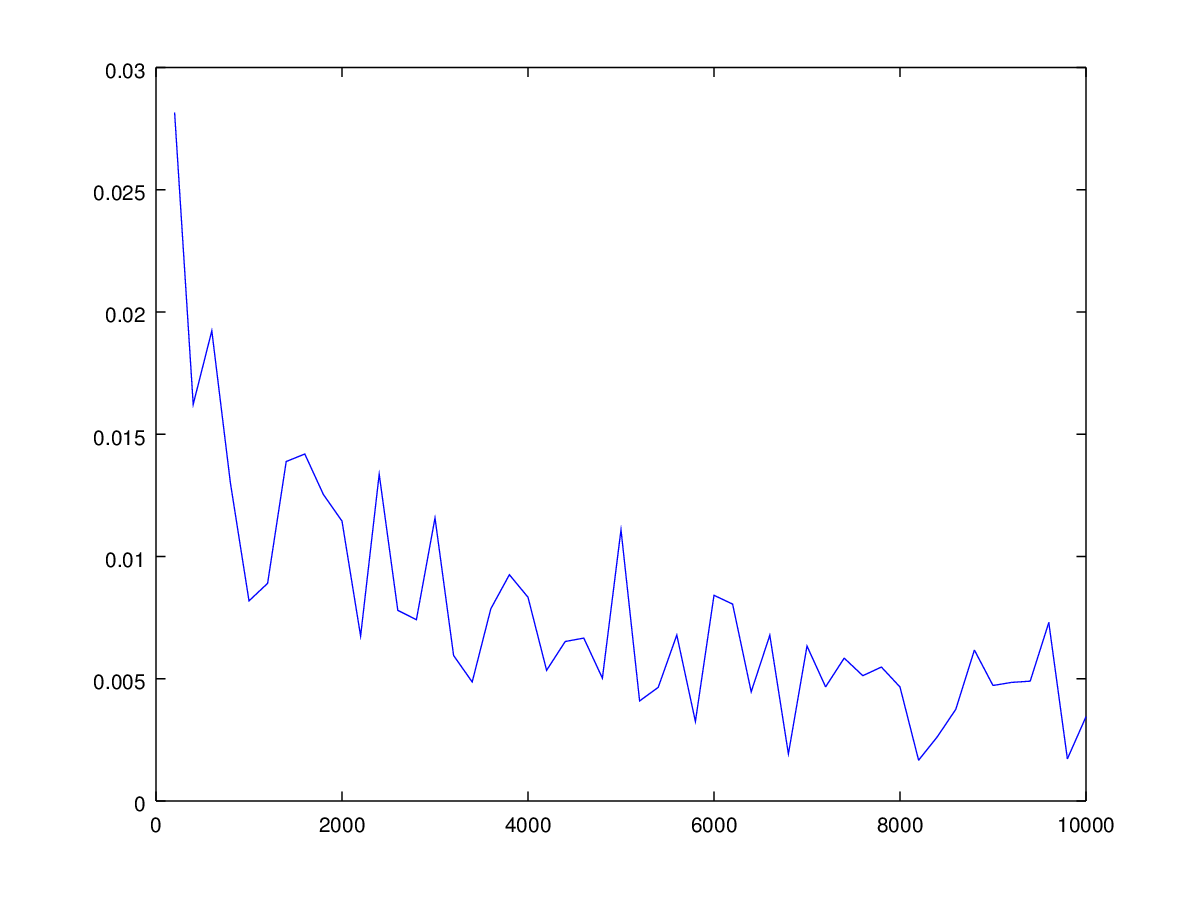
В [2] приводится формула с весом: $$\int_a^b f(x)\, dx = \int_a^b \frac{f(x)}{p(x)}p(x)\,dx = \int_0^1 \frac{f(x(\xi))}{p(x(\xi))}\,d\xi,$$ где $$\xi(x) = \int_a^x p(x)\,dx, \quad \int_a^b p(x)\,dx = 1.$$ Плотность распределения $p(x)$ выбирается так, чтобы $f/p$ было примерно постоянным на $(a,b)$, тогда все элементы выборки вносят примерно одинаковый вклад в сумму.

Формула для вычисления интеграла: $$\int_a^b f(x)\, dx \approx \frac{b-a}{N}\sum_{i=1}^N \frac{f(x_i)}{p(x_i)}, \quad x_i = \xi^{-1}(R_i).$$ Здесь выборка $R_i$ распределена по закону $R(0,1)$.

Генерация случайной величины с заданным законом распределения

Источники:

1. Генераторы непрерывно распределенных случайных величин, Хабрахабр.
2. Сборник задач по математике для втузов. Часть 3. ТВ и МС. Под ред. А.В. Ефимова. - М.: Наука, 1990.

Пусть $F(x)$ -- заданная функция распределения.

Алгоритм:

1. Сгенерировать выборку $y_i$ с распределением $R(0,1)$.
2. Найти $x_i = F^{-1}(y_i)$.

Код:

# Датчик случайной величины с распределением Лапласа
function ret = gen_laplace()
  y = rand;
  ret = laplace_inv(y);
endfunction

# Датчик случайной величины с нормальным распределением
function ret = gen_normal()
  y = rand;
  ret = norminv(y);
endfunction

N = 25000;
sample_laplace = sample_normal = zeros(1, N);

for i = 1 : N
  sample_laplace(i) = gen_laplace();
endfor
figure
hist(sample_laplace, 40);

for i = 1 : N
  sample_normal(i) = gen_normal();
endfor
figure
hist(sample_normal, 40);

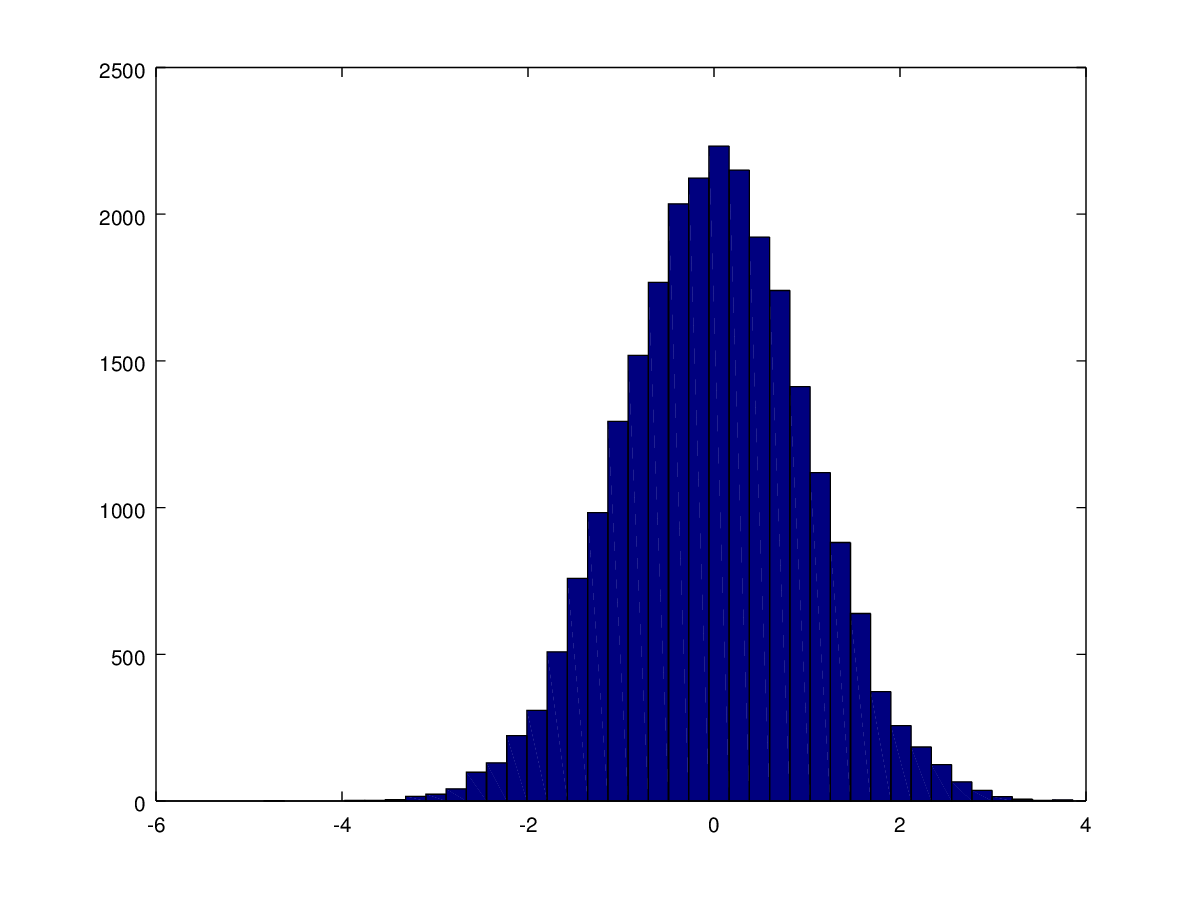
Гистограмма, построенная по датчику случайной величины с распределением Лапласа:

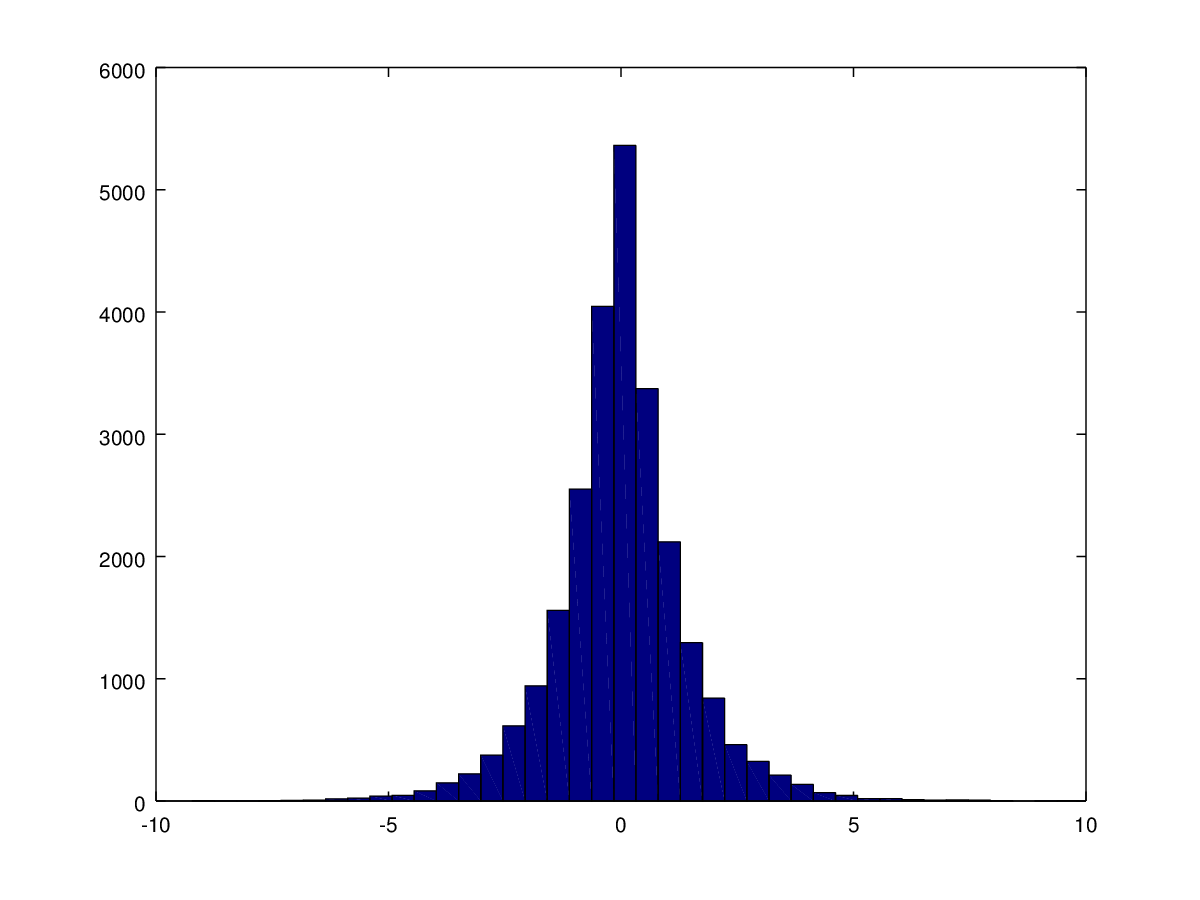
Гистограмма, построенная по датчику случайной величины с нормальным распределением: